Contribución:
Lic. Ec. Rocío Mariel Cerino
Lic. Ec. María Emilia Bullano
Lic. Geog. Natalia Raptópulos,
Infraestructura de Datos Espaciales Córdoba (IDECOR)
25 de noviembre 2020.
Durante los meses de octubre y noviembre, IDECOR en cooperación con la Facultad de Ciencias Exactas, Físicas -y Naturales (FCEFyN) de la Universidad Nacional de Córdoba llevó adelante una experiencia piloto de mini cursos virtuales, dirigidos al desarrollo de competencias específicas en la comunidad de usuarios de IDECOR.
Entre el 26 de octubre y el 16 de noviembre se llevó adelante el curso “Métodos de interpolación usando R” cuyo objetivo principal fue aprender cómo obtener estructuras continuas de datos territoriales, cuando sólo se dispone de algunas observaciones georreferenciadas.
Los cursos fueron dictados por el equipo de Modelización de IDECOR, conformado por el Mgter. Juan Pablo Carranza, el Mgter. Federico Monzani, la Lic. Ec. Rocío Mariel Cerino y la Lic. Ec. María Emilia Bullano, y contó con el apoyo de la cátedra de Sistemas de Información Territorial de la FCEFyN de la UNC. Como se trató de una experiencia piloto, la participación fue por invitación, a alumnos de la cátedra y al personal técnico de las áreas de gobierno que trabajan proyectos especiales con IDECOR.
Las grabaciones de ambos encuentros están disponibles en el Canal de YouTube de IDECOR y desde el siguiente link puede accederse a los script con los códigos utilizados en ambas clases.
Interpolación espacial
La interpolación espacial se basa en el cálculo de los valores desconocidos de una variable espacial a partir de otros valores conocidos (muestra).
Un primer conjunto de técnicas para resolver este problema se encuentra en la geoestadística. Durante el curso se desarrollaron aplicaciones de Kriging Ordinario, Kriging con tendencia y Regression Kriging y se llevó adelante una experiencia paso a paso utilizando el lenguaje de programación R (Imagen 1).
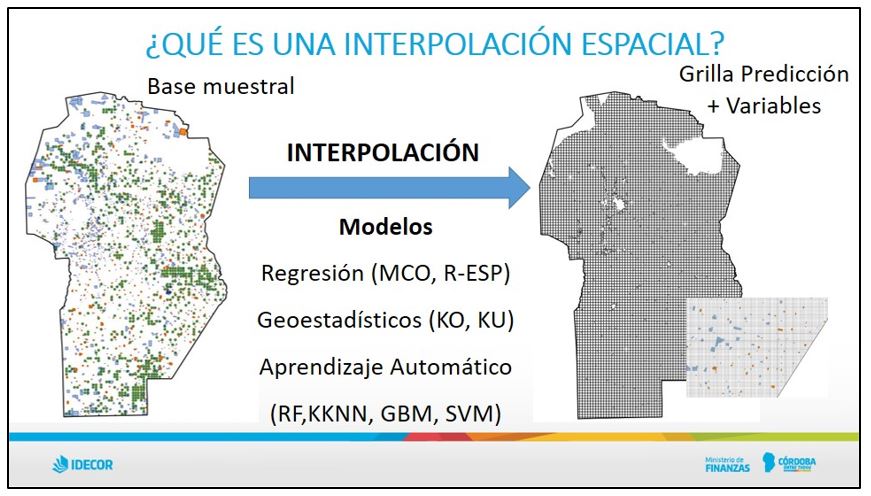
El segundo grupo de estrategias se centra en técnicas algorítmicas; en particular, durante el curso se profundizó en el uso de Kernel K-nearest Neighbors y también se llevó adelante una experiencia paso a paso con el lenguaje de programación R (Imagen 2).
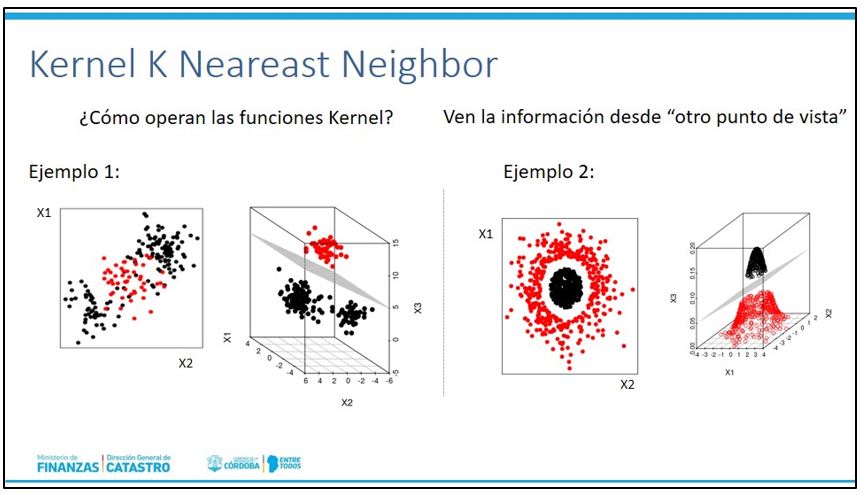
¿Qué es la interpolación geoestadística Kriging?
El Kriging es una técnica geoestadística que permite realizar interpolaciones espaciales y predecir los valores de la variable en sitios no muestreados. Parte del principio que los puntos más próximos en el espacio tienen valores más parecidos a aquellos que están más alejados (Ley de Tobler, 1970). La relación de estos puntos se ve a través de un semivariograma y supone que la variabilidad depende del espacio. Un semivariograma es una función que describe la variabilidad espacial de un fenómeno, de manera que mientras más similares sean las observaciones, menor la semivarianza. Se asume en este contexto que la variable muestral se distribuye en forma normal, con media estacionaria y varianza σ^2.
Es posible aplicar distintos tipos de Kriging: Kriging Ordinario, Kriging Universal, Kriging con tendencia y Regression Kriging. Elegir cuál aplicar es el primer paso para hacer una interpolación espacial de este tipo. El segundo, es estimar el semivariograma empírico y luego elegir el modelo que mejor se ajuste (gaussiano, esférico, exponencial, etc.). Por último, se aplica el cálculo de Kriging con el fin de obtener la interpolación (superficie continua).
En el mapa más abajo (Imagen 3) se puede observar una muestra de datos y el resultado obtenido mediante la interpolación con Kriging Ordinario.
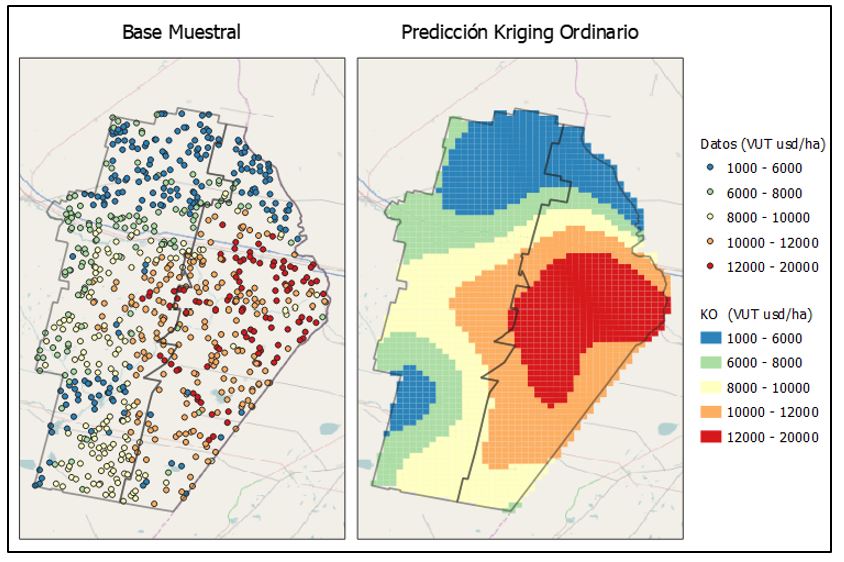
En el mapa que sigue (Imagen 4) se puede apreciar la interpolación mediante Kriging Universal, particularmente Regression Kriging, sumando las variables materia orgánica ( ) distancia a puerto ( ), distancia a centros urbanizados ( ) y distancia a centros de acopio ( ).
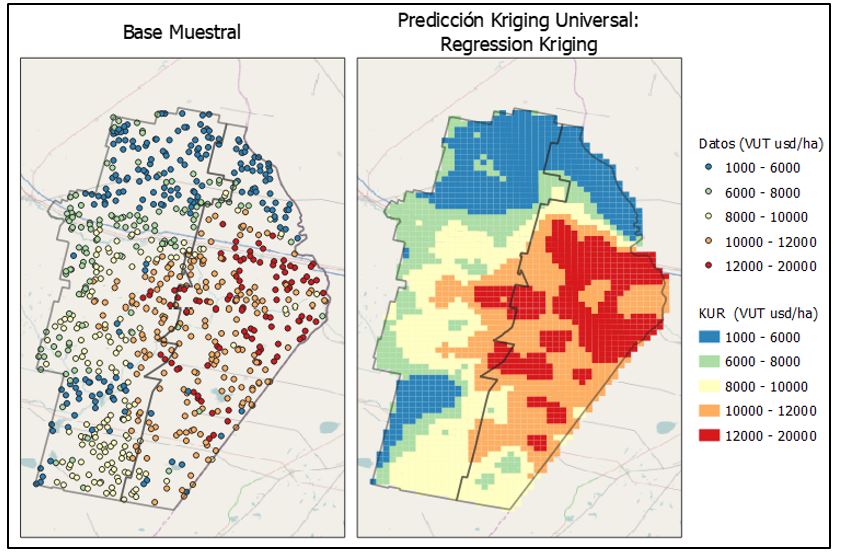
¿Qué son las técnicas algorítmicas de interpolación espacial?
La ventaja de estas técnicas frente a las propuestas por la geoestadística es que son no paramétricas, es decir que no presuponen ninguna distribución funcional de los datos. La interpolación mediante el algoritmo Kernel K Nearest Neihgbor (KKNN) predice los valores de acuerdo al de sus K pares más cercanos. Resulta relevante aclarar que la definición de cercanía responde a una distancia en una hiperplano (distancia euclidiana, no distancia geográfica). Por lo que el valor de K resulta determinante a la hora de realizar la interpolación. Dado que se quiere obtener un resultado con el mínimo error de predicción, una forma de obtener el valor de K es mediante un proceso de validación cruzada con el fin de determinar el valor que minimiza el error de predicción.
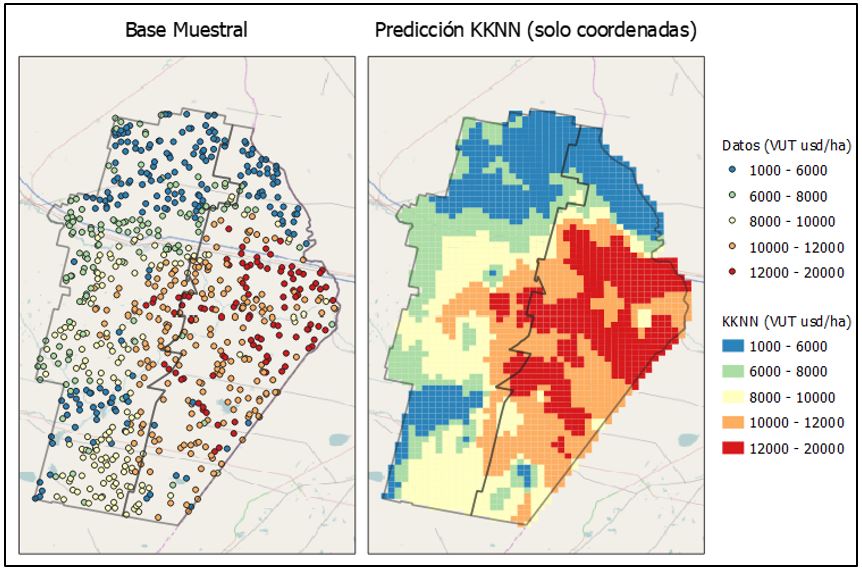
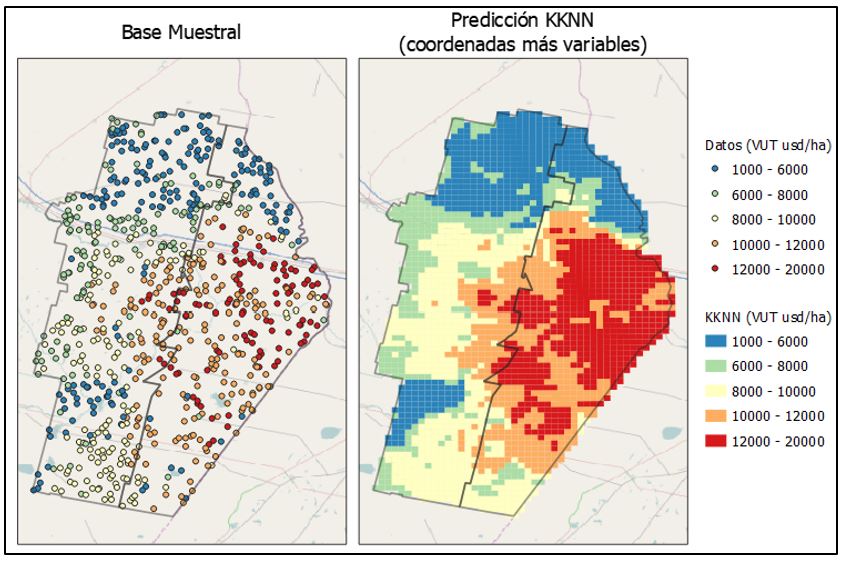
En las imágenes presentadas a continuación se puede observar los puntos muestrales (izquierda) y el mapa con las interpolaciones sobre la grilla de predicción (derecha). La Imagen 5 presenta el resultado de aplicar la técnica KKNN donde las variables independientes son las coordenadas geográficas (x, y). Por su parte, en la Imagen 6 se puede apreciar el mapa derivado de interpolar con KKNN pero agregando más variables independientes: materia orgánica, distancia a puerto, distancia a urbanizaciones, distancia a centros de acopio (además de las coordenadas).
Pensando los próximos pasos…
La selección de la temática de este primer curso nace de la inquietud y necesidad de muchos usuarios de IDECOR que enfrentan el desafío de transformar datos muestrales en superficies continuas. Esto pasa, por ejemplo, cuando se manipulan datos climáticos de algunas estaciones meteorológicas y se necesita trasladarlos a todo el territorio de la provincia. También, por ejemplo, en Estudio Territorial Inmobiliario que desarrollan el Catastro Provincial e IDECOR, donde se aplican estas técnicas en el desarrollo de los mapas de valor del suelo y otras variables temáticas, como el rendimiento de la actividad agrícola o los arrendamientos rurales, entre otros.
Esperamos 2021 sea un año con más acciones de capacitación y aprendizajes que sumar. Te invitamos nos escribas compartiendo tus necesidades e intereses, a fin de considerarlas en el diseño del Plan de Trabajo 2021. Escribirnos a [email protected]
Para mantenerte informado, seguí a IDECOR por Instagram en idecor.ok y los materiales de capacitación, en el canal de YouTube IDECOR.




