Contribución:
Ing. Aldo Algorry
Profesor e investigador de la Universidad Nacional de Córdoba
Responsable de Tecnología y Base de Datos
IDECOR
13 de noviembre 2019
La topología, y en especial las reglas topológicas, constituyen herramientas fundamentales para asegurar y mejorar la calidad de los datos geográficos en una base de datos espacial.
En este post brindamos una introducción a los conceptos y funcionalidades principales para administrar mejor con nuestros datos y asegurar mayores niveles de calidad, que impacten positivamente en los productos y decisiones que se toman con los datos que publicamos a través de las IDE.
Reglas topológicas en una base de datos espacial
Las reglas topológicas se validan a través de relaciones espaciales entre dos objetos del mismo tipo o de distinto tipo y se evalúan en función de las geometrías que los conforman. Tienen la particularidad de mantenerse invariables en las transformaciones de rotación, traslación y escala. Reglas como: “Un eje de calle no puede cortar una manzana”, “Una parcela debe estar totalmente dentro de una manzana”, “Un barrio no puede solaparse con otro barrio”, entre otras, constituyen reglas topológicas que deben ser verificadas para que no se produzcan inconsistencias espaciales.
La definición de las reglas surge del proceso de diseño de la base de datos y del análisis de la realidad territorial que queremos registrar.
En una base de datos espacial 2D encontramos con tres tipos de geometrías básicas: puntos, líneas y polígonos. Estas geometrías se vinculan espacialmente mediante relaciones espaciales: “se tocan”, “no se tocan”, “se intersectan”, “una incluye a la otra”, etc. Estas relaciones se pueden definir de una manera formal usando la llamada matriz “DE-9IM ”.
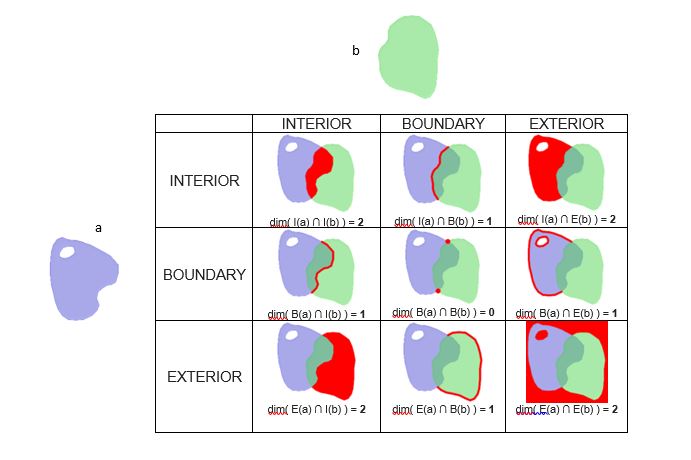
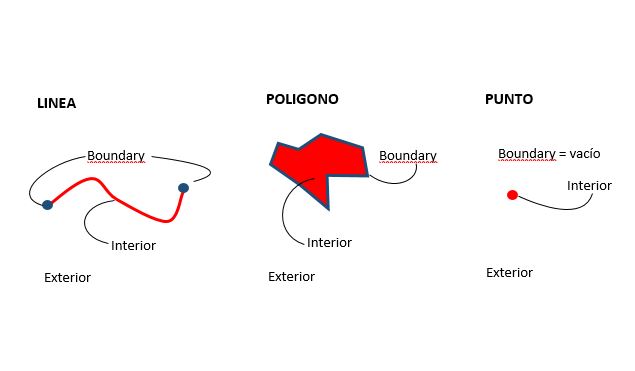
Para ello en cada tipo de geometría se definen tres partes: “Interior”, límite que llamaremos “Boundary” y “Exterior” como se indica en la figura 1, donde se define el significado de cada parte para los puntos, líneas y polígonos existentes en la base de datos espacial.
Las partes de diferentes geometrías se pueden vincular de diferentes maneras, definiéndose así, formalmente la relación espacial entre dos geometrías. Por ejemplo, en dos líneas que se cruzan, la intersección de sus “interiores” es un punto; en este caso se dice que se vinculan por un objeto de dimensión 0 (punto). En el caso de un polígono que se superpone con otro, donde su “Interior” se intersecta con el “Boundary” del otro polígono formando una línea, se dice que forman un objeto de dimensión 1 (línea), mientras que los interiores de ambos polígonos forman un polígono de 2 dimensiones.
Cuando sólo se exige alguna intersección sin que se indique su dimensión, se utiliza el símbolo “T” (True) que equivale a cualquier dimensión de la intersección, 0, 1 o 2. También puede suceder que dos partes de dos geometrías no se intersecten de ninguna forma; por ejemplo, en el caso de dos polígonos donde uno se encuentra completamente dentro del otro sin tocarse los límites (el “boundary” del polígono externo no se toca de ningún modo con el “interior” del polígono interno). Estas relaciones se indican como “-1” o con “F” (False).
Por último, pueden definirse relaciones espaciales donde la relación entre dos partes de dos geometrías no sea relevante. Por ejemplo, si queremos definir una relación espacial donde dos polígonos se “tocan” de alguna forma, la relación entre los “interiores” puede ser cualquiera (incluida ninguna), ya que con que se intersecten los “boundaries” es suficiente; en este caso se utiliza un “*” (asterisco) que indica que la relación es de dimensión -1, 0, 1 o 2.
Matriz de relaciones espaciales
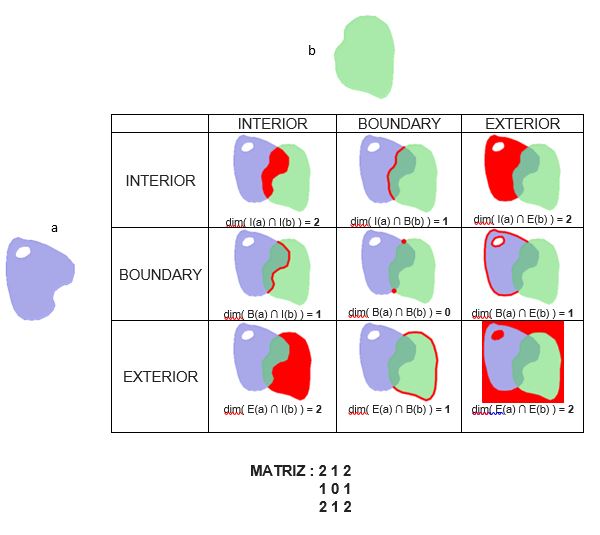
A partir de definir las relaciones entre las partes se puede construir una matriz de doble entrada (DE-9IM) que indique el tipo de intersección que tienen o deben cumplir las partes para validar una relación entre dos geometrías; de este modo, se genera una descripción formal de una regla topológica susceptible de ser verificada por un sistema computarizado como un motor de base de datos espacial.
Si “a” y “b” son dos geometrías y E(a), B(a), I(a) y E(b), B(b), I(b) sus exteriores, boundaries e interiores respectivamente, podemos definir la matriz DE-9IM como:

En la figura 2 se muestra un ejemplo de la matriz para dos polígonos (a y b) que se intersectan.
La matriz puede tener variados usos; por ejemplo, para buscar o filtrar en la base de datos pares de geometrías que cumplan (o no) con determinada matriz, o puede usarse como regla topológica para un control de inconsistencias.
Como ejemplo de la formación de una regla topológica tomemos el caso de quien registra en una base de datos espacial un lago (polígono) y muelles (líneas) que acceden al lago. Podemos definir algunas reglas que se deben cumplir, para que no existan inconsistencias geográficas.
- Todos muelles deben entrar en un lago.
- Los muelles no pueden estar totalmente dentro del interior del lago.
- Los muelles no pueden estar totalmente fuera del lago.
- Un extremo de los muelles debe estar sobre el límite del lago.
- Un extremo de los muelles debe estar en el interior del lago.
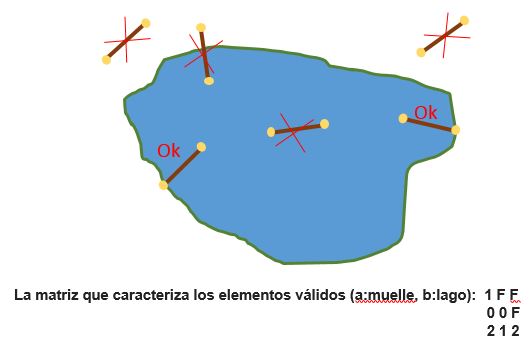
Las bases de datos espaciales como PostGIS soportan la realización de consultas donde se provee la matriz DE-9IM y se obtienen los pares de objetos que cumplen con determinada regla topológica, lo que nos permite asegurar calidad de los datos geográficos y realizar controles de consistencia gráfica.
El contenido de este artículo forma parte del curso “Introducción a las bases de datos espaciales” que dicta periódicamente IDECOR (acceder al material en https://www.idecor.gob.ar/wp-content/uploads/2018/07/CursoPostGIS-1-1.pdf).