Colaboración:
Mg. Lic. Federico Monzani,
IDECOR
15 de febrero de 2023
¿Qué es una interpolación de datos geoespaciales? ¿Para qué se usa? ¿Cómo la aplicamos en IDECOR?
La palabra interpolar proviene del latín interpolare que quiere decir recomponer, intercalar o cambiar. En la matemática o estadística esta palabra se usa para expresar cálculos o estimaciones de valores de una variable dentro de su dominio. A modo de ejemplo, la tasa de interés se usa para interpolar los valores de capital en el tiempo, es decir llevar los valores del presente al futuro o traer los valores del futuro al presente.
De la misma manera que la tasa de interés “en el tiempo”, actúan las coordenadas en el espacio. A través de ellas, y por medio de alguna técnica geoestadística, se estima el valor de la variable “en el espacio”.
En IDECOR se trabaja con distintas técnicas de interpolación espacial, como métodos geoestadisticos o de aprendizaje computacional para inferir el valor de variables en el territorio, en el marco proyectos o estudios para diversos organismos. Por ejemplo, en el espacio rural, se estiman rendimientos de cultivos (soja y maíz, en qq/ha), valores unitarios de la tierra ($/ha), propiedades del suelo (materia orgánica, pH, fósforo), entre otras, generalmente en unidades espaciales de 25 hs (grilla regular de 500 m de lado) y para todo el territorio provincial. También se realizan este tipo de análisis en el ámbito urbano, en diferentes temáticas.
En esta nota repasamos algunos principios de los métodos geoestadisticos para estimar variables y los aplicamos a un ejemplo concreto, para observar la distribución espacial de la materia orgánica del suelo dentro de un lote rural.
La técnica geoestadística Krige
El método Krige, también conocido como kriging, fue desarrollado por el ingeniero sudafricano Danil Gerhardus Krige (1919-2013) con el objetivo de evaluar los recursos mineros (básicamente encontrar pepitas de oro) y fue formalizado en la década del ‘60 por el ingeniero francés Georges Matheron.
Esta técnica estadística surge como una evolución de la estadística clásica al contemplar el espacio en relación a la localización; situación que la estadística frecuentista no contempla, porque parte de otros supuestos (covarianza es distinta de cero).
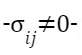
Esto hace necesario utilizar otro tipo de herramientas que permitan incorporar la ubicación geográfica de los datos.
A grandes rasgos la geoestadística se basa en los siguientes principios:
1. Es una técnica de interpolación lineal.
2. Se fundamenta en la primera ley geográfica de Tobler “donde todo está relacionado con todo lo demás, pero las cosas más cercanas están más relacionadas que las cosas distantes”. Bajo este principio los puntos más próximos en el espacio tienen valores más parecidos que aquellos que están más alejados.
3. Se basa en el supuesto que la variable independiente se distribuye de manera normal:
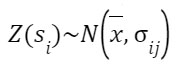
que es dependiente del espacio, con media constante (estacionaria) y varianza – covarianza (dependiente de la distancia y dirección); donde la variable
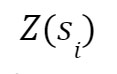
es el valor que asume la variable en los puntos geolocalizados s1, s2, …, sN para N datos (s = spatial = espacial)
4. El Modelo:
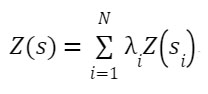
es una combinación lineal de funciones aleatorias independientes Z(si); donde i, son los ponderadores de la combinación lineal, que surgen de minimizar la varianza y para que ello se cumpla debe suceder
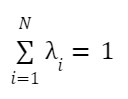
5. Si lo de arriba sucede, los estimadores obtenidos son ELIO –estimadores lineales insesgados óptimos.
6. El proceso es estacionario de segundo orden, media y varianza constante, donde su covarianza varía en función de la distancia entre dos puntos geoposicionados, que se reflejan en la función de semivariograma.
El concepto clave de la técnica krige, donde radica su creatividad, es el semivariograma que refleja el principio que “las cosas más cercanas en el espacio son más predecibles y tienen menos variabilidad”, mientras que las cosas distantes son menos predecibles y están menos relacionadas. Matemáticamente esto se expresa por medio de una función de semivariograma, que mide el grado de dependencia espacial entre dos puntos a través del grado de variabilidad.
Dos puntos cercanos, en función de la ley de Tobler, deberían ser más semejantes (relacionados) y menos variables, que dos puntos más alejados. Desde el punto de vista matemático, la función semivariograma se expresa de la siguiente manera:
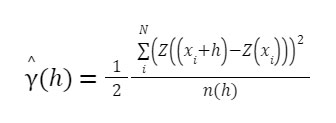
Esquemáticamente las ideas se pueden representar de la siguiente manera:
En suma, existe un semivariograma empírico mediante el cual se estiman los parámetros del semivariograma teórico. Estos parámetros son:
Rango: mide la distancia donde la función semivariograma llega a su máximo.
Nugget o Efecto Pepita (por pepita de oro) es el valor del semivariograma cuando la distancia es cero (ordenada de origen).
Partial–Sill: el umbral, es decir donde la variabilidad entre dos puntos llega a ser máxima.
Las funciones del semivariograma teórico más utilizadas son: Exponencial, Esférica o Gaussiana. Esto es debido a que este tipo de funciones reflejan la idea que los puntos más cercanos, a menor distancia, tienen menor variabilidad que los puntos más lejanos. Esta variabilidad crece por lo menos en su última etapa (mayor distancia), a tasas decrecientes, hasta alcanzar el umbral (partial sill), donde la distancia del rango resulta ser máxima y esa variabilidad se vuelve intrascendente.
Dentro del modelo krige existen distintas técnicas de estimación. Entre las más conocidas se encuentra Krige Ordinario, que considera como variable sólamente las coordenadas, resultando un modelo simple y parsimonioso. Co-krige resulta una extensión de la técnica krige al método multivariado, es decir considerar otras variables además de la variable objetivo. Krige Universal, los modelos Krige suponen estacionariedad de segundo orden (media y varianza constante), es decir que hacia todas las direcciones espaciales no se observa una tendencia. En caso que existiera una tendencia de la variable de estudio hacia alguna dirección en el espacio se debe corregir, modelando la tendencia a través sus coordenadas. También, con el objeto de mejorar el ajuste de los modelos, se suele corregir la tendencia reflejada en el espacio por la existencia de alguna covariable; surgen así las técnicas de krige con regresión o krige con deriva.
Un ejercicio para aplicar a cualquier temática
Desarrollaremos un caso práctico, donde se estimarán los niveles de materia orgánica (MO) para un determinado lote o área de interés, a partir de un conjunto de muestras de suelo distribuidas en la zona.
En una primera instancia se toman muestras de suelos registrando su posición (latitud y longitud). Luego, a través de un análisis químico de laboratorio, se determina el contenido de MO en la profundidad de extracción, normalmente 20 cm. El muestreo geoposicionado puede realizarse fácilmente por medio de alguna aplicación celular de acceso libre (IDECOR LandCollect, KoboToolbox, Qfield, entre otras).
Figura 1. Distribución espacial de muestras de materia orgánica en un lote o zona de estudio.
En este ejemplo se extrajeron 15 observaciones georreferenciadas en un lote de 165 ha, lo que refleja una muestra cada 11 ha (Figura 1). Aunque en términos estadísticos mientras más grande el tamaño de la muestra mejor, generalmente por un principio de costo y practicidad, la toma de muestra es limitada. La Tabla 1 contiene las características de las mismas: mínimo de 1.50%, media 1.76% y máximo 1.92%, con un coeficiente de variación del 6% de MO.
Tabla 1. Estadística descriptiva de la muestra MO
| Obs | mínimo | 1er quantil | mediana | media | 3er quantil | máximo | sd | cv |
| 15 | 1,59 | 1,675 | 1,77 | 1,764 | 1,85 | 1,92 | 0,11 | 6% |
Recopilada la muestra, se interpola a cada una de las celdas por medio de la técnica krige ordinario, resultando el siguiente semivariograma y los consiguientes estimadores de parámetros:
Con los estimadores de los parámetros (nuegget, parcil sil, ranger, modelo Gasussiano) se calcula la función de semivariograma para estimar el modelo y de ese modo predecir los distintos valores en las celdas de la grilla de 25 ha definida (Figura 2).
Figura 2. Distribución espacial de MO en el lote.
Con el objeto de observar la calidad de ajuste del modelo se calculó el RMSE (root-mean-square error –raíz cuadrada de la media al cuadrado de los errores-) que resultó 0.0075. El RMSE se interpreta como la variabilidad no explicada del modelo en promedio y se encuentra en la misma unidad de la variable respuesta, es decir MO.
Tabla 2. Estadística descriptiva de la predicción
| Obs | mínimo | 1er quantil | mediana | media | 3er quantil | máximo | sd | cv |
| 713 | 1,59 | 1,72 | 1,77 | 1,76 | 1,8 | 1,93 | 0,066 | 4% |
La tabla 2 refleja la estadística descriptiva de la predicción. Se estimaron valores de MO en 713 celdas, obteniéndose un valor mínimo de 1,59%, máximo de 1,93 %, mediana y media muy semejantes de 1,77 % y 1,76%, y un coeficiente de variación del 4%.
La interpolación a través de krige ordinario permite obtener información sobre la distribución espacial de la MO en el lote. Sin embargo, es de gran importancia la observación profesional in situ, que ayuda a comprender la variabilidad del lote y contrastar los resultados de la modelización en el territorio.
Conclusiones finales
Krige es una técnica geoestadística que permite interpolar cualquier variable en dominios espaciales continuos y, de ese modo, observar su estructura espacial. Lo que resulta interesante de esta técnica es que trabaja con la variable objetivo y las coordenadas como variables independientes y, de ese modo, reduce los costos de obtener o calcular otras variables. Para mejorar la predicción y el ajuste del modelo, se suelen utilizar otras variables (co-variables) que, a través de la introspección u observación de matriz correlación (entre otras técnicas), se considere que puedan afectar la variable independiente. Para ello surgieron las técnicas de co-krige, Krige con deriva o regresión. Además, resulta atractivo hacer interpolaciones lineales que parten de funciones no lineales del semivariograma.
Para trabajar con esta técnica, existe una amplia gama de software libre que la contemplan, como R (en sus librerías gstat, sp, caret, entre otras), QGIS (librerías SAGA), Infostat (desarrollado en la Facultad de Ciencias Agropecuarias de la UNC) que tiene un módulo dedicado a krige, fastMapping, una aplicación libre generada para mapear variables espaciales, entre otros.
Te dejamos algunos recursos adicionales para profundizar e iniciarte en forma práctica en este tema. Por consultas o inquietudes, puedes escribirnos a [email protected].
Para mantenerte informado sobre las novedades de IDECOR, seguinos en Instagram en idecor.ok y en nuestro canal de YouTube.
Bibliografía y recursos adicionales
“Miniguías para Aprender: métodos de interpolación usando R”. Ver nota
1er Curso virtual IDECOR – Interpolación mediante técnicas geoestadísticas usando R. Ver curso
2° Curso virtual de IDECOR: Interpolación mediante técnicas algorítmicas usando R. Ver curso
Viera, M. A. D., & González, R. C. (2002). Geoestadística aplicada. Instituto de Geofísica, Universidad Nacional Autónoma de México, Ministerio de Ciencia, Tecnología y Medio Ambiente de Cuba: México DF, México, 31-57.